Se ha dicho que muchas son las causas que impulsaron la creación de un sistema de comunicaciones que permitiera la transmisión de información a distancia sin demasiadas complicaciones.
En una comunicación telefónica, al hablar una persona, la señal de ondas generadas circula a través de conductores hacia el otro abonado, pero ¿Por qué son necesarios los cables?
La respuesta es que la señal de audio (baja frecuencia) no puede irradiarse a través del espacio con costos accesibles, razón por la cual se intenta “montar” dicha información sobre una portadora de RF más fácil de propagar por el aire.
Además, si se quiere transmitir la información de varias personas en forma simultanea por distintas emisoras, las señales se mezclarían por ser todas de audio y resultaría imposible para un receptor separar una de otra. Este inconveniente se soluciona “modulando” a diferentes portadoras (cada una de distinta frecuencia) con cada información; de esta manera el receptor deberá primero reconocer a la portadora deseada y una vez logrado esto se le extrae la información.
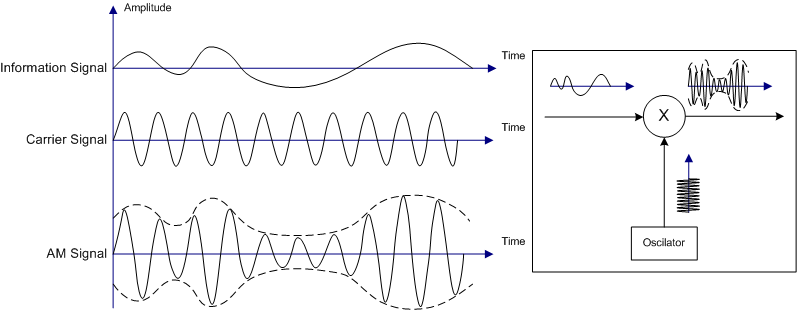
Recuerde que “modular” significa cambiar algún parámetro de una señal llamada “portadora”, para ello se emplea otra señal llamada “información” y que el objeto de la modulación es poder transmitir una información de baja frecuencia a través del espacio, que como vehículo utiliza una señal portadora.
Para continuar con el tema veamos algunos conceptos.
En una señal de AM, la modulante es la variación de la amplitud de la portadora. Para obtener la expresión matemática de una señal de AM debemos definir la expresión de la portadora y la expresión de la modulante:
- Modulante
em (t) = Am sen ωm * t
Donde:
em (t) = Tensión instantánea de la modulante
Am = Amplitud de pico de la modulante
ωm = Pulsación angular de la modulante (2 π fm)
- Portadora
ep (t) = Ap sen ωp * t
Donde:
ep (t) = Tensión instantánea de la portadora
Ap = Amplitud de pico de la portadora
ωp = Pulsación angular de la portadora
Si la señal de AM la llamamos X(t), en ella la amplitud máxima de la portadora Ap será variable al ritmo de la modulante em(t); es decir:
X(t) = (Ap + em(t)) sen ωp * t
A la amplitud de la portadora se le ha sumado la señal modulante, que es precisamente la definición de AM.
Desarrollando la formula anterior:
X(t) = [Ap + Am sen (ωm * t)] * sen (ωp * t)
Si le aplicamos la propiedad distributiva:
Ecuación 1
X(t) = {[Ap * sen (ωp * t)] / A} + {[Am sen (ωm * t) * sen (ωp * t)] / B}
Puede observar en la expresión de la señal de AM que el termino (A) es la señal portadora, mientras que el segundo término es aquel que contiene a la información y debemos desarrollarlo matemáticamente para entender que es lo que representa.
Una regla trigonométrica expresa que:
sen α * sen β = 1/2 (cos (α + β) – cos (α – β)
Aplicando esto en el término (B) de la ecuación 1 se tiene:
X(t) = Ap sen (ωp * t) + Am {[cos (ωp + ωm) * t – cos (ωp – ωm) * t] / 2}
Desarrollando:
X(t) = Ap sen (ωp * t) + [(Am / 2) cos (ωp + ωm) * t] – [(Am / 2) cos (ωp – ωm) * t]
Lógicamente esta expresión puede representarse en el campo del tiempo y en el campo de la frecuencia.
Veamos un ejemplo, analicemos el comportamiento en función de la frecuencia, de una portadora de 100KHz modulada con la voz de un locutor. Para hacer este análisis debemos saber cuál es la forma “promedio” de la señal correspondiente a la vos humana. Es sabido que el espectro de frecuencia audible abarca frecuencias comprendidas entre 20 Hz y 20 KHz, la voz humana también reproduce señales en esta gama de frecuencias pero lo hace con mayor intensidad para frecuencias medias decreciendo para tonos graves y agudos. De esta manera se podría hacer un análisis espectral de vos humana promedio, lo que arrojaría el resultado como la figura 1.
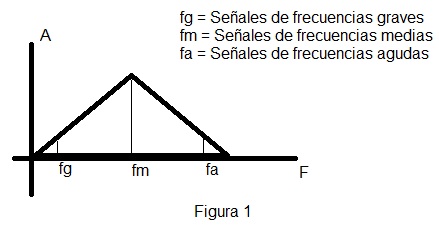
Note que para frecuencias medias se tiene una amplitud máxima, además, es una curva continua, lo que indica que al habla pueden generarse señales de todas las frecuencias dentro del espectro audible. Siguiendo con nuestro ejemplo, digamos que cada frecuencia de la voz del locutor modulara a la portadora, sumándose y restándose respectivamente con dicha portadora. Por lo tanto, esto resultara que la información aparezca en ambos lados de la portadora sin distorsión pero con la mitad de la amplitud. Es decir, la información aparece por duplicado en bandas que están a los costados de la portadora. A estas bandas, que aparecen en los laterales de la portadora y contienen la información, se les denomina bandas laterales. La banda que se ubica por encima de la portadora se denomina Banda lateral superior (BLS), y la que está por debajo, banda lateral inferior (BLI).